Day 1: Introduction

Random Walk Character of Polymers

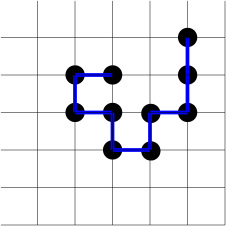
		Polymers can be considered random walks, if looked at on the appropriate scale. We will exploit this quite heavily not only from an analytical point of view, but also for computational methods. To give you an idea of what is involved lets make small detour: We assume a lattice. For simplicity we take a simple square lattice. On this lattice a particle or walker is placed. The walker regards this initial position as the origin. The walker draws a random number and decides, according to the drawn random number, to go to a new position on the lattice. The new position must be one of the nearest neighbors and each of the neighbors has the same probability to be visited. Once he is at the new position, the walker regards this position as his new origin. In other words, he immediately forgets where he came from. Every step is made as if it is the first step. All steps are then independent of each other. Schematically a walk is shown in the following picture.
		Example of a random walk in on a square lattice.

Random Walk Character of Polymers