Let denote the transition probability to move from state x to the state x’. A sufficient condition to reach equilibrium and that the states are distributed according to the desired distribution

P(x) is the microscopic reversibility or detailed balance

Here P is the equilibrium distribution. This condition is very much like the time reversibility in the newtonian equation of motion! It alone does not yet guarantee that the states are distributed in the correct way. We also require that every state can be reached! We do not want the available phase space to separate into disjoint parts. Further, once in a state, the probability to jump to any state must be one. That is to say, the probability to jump is a sure event.

From the above condition we can immediately derive the functional form of the transition probabilities, given the equilibrium distribution. The transition probability must have two parts. There is one part that proposes a new state. A new state x' is proposed with the probability . The other part of the transition probability deals with the acceptance of the proposed change. This is an important point. We propose a change of the state with a certain probability and the proposition is accepted with a probability that we call . We define the transition probability W as

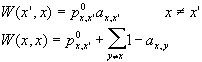
Form this definition and the condition of the detailed balance we get

for the only interesting case that the two states are not equal. Hence we can define as a function F with the argument

to find that F needs to satisfy the following relation