Random Walk

• Growth: Starting from a seed site, we grow the chain up to length N by choosing a nearest neighbour site at random. Each of the four site on a simple square lattice is a legitimate new growth site. Hence, there is no excluded volume interaction!
• Reordering: Starting from a straight line of N nearest neighbour sites, the chain can develop into a new conformation by:
  
  Reptation: We take away from one end of the chain a site and add this to the other end by randomly selecting a nearest neighbour-site of the end site.
  
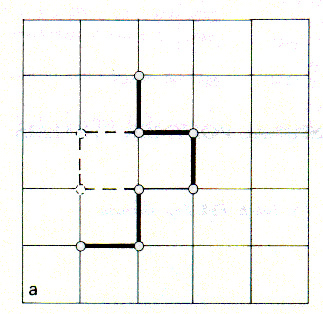
  Rotation: We select at random a site along the chain. We use this site to rotate one half of the chain around the selected site
  
  Kink and Crank-Shaft: Kinks are flipped  and two connected sites can flip

It is very easy to simulate a random walk on the computer. The following program segment generates such random walks.

Program Random Walk:

It is assumed that in the array random are stored numbers which are uniformly distributed in the interval (0,1). A random number from the array is then multiplied by 4 and converted to an integer value. This integer value can either be 0,1,2 or 3 labeling the four possible directions or nearest neighbors on the square lattice. The numbers 0,1,2 and 3 are uniformly distributed as long as the numbers in the array random are so distributed. Depending on the direction the random number points to, the walker occupies the appropriate position on the lattice by increasing or decreasing the x or yvariable. The variables xn and yn hold the new position of the random walker.  This program generates random walks on a square lattice.

/* ---- Choose a new nn site ---- */
i = floor(random[index++]* 4.0);
switch (i) {
    case 0: xn = x-1;
            yn = y;
            break;
    case 1: yn = y-1;
            xn = x;
            break;
    case 2: yn = y+1;
            xn = x;
            break;
    case 3: xn = x+1;
            yn = y;
            break;
} /* ---- switch i ---- */