A number of statistical tests have
been devised to check for the properties of random number generators. To name just a few
prominent tests
- c2
- Kolmogorov-Smirnov,
- correlation,
- run and
- visual test.
The statistical tests are tests how well the empirical distribution,
i.e., the generated sequence, fits a test distribution. Of these, we will not describe any
and direct the reader to the literature. We shall discuss, however, the run testt.
The run test tests whether an empirical distribution has monotone decreasing or
increasing subsequences and confronts these with the expectation for their occurrence. Let
us assume that we want to test for monotone increasing subsequences. Such a test is called
a run test up, otherwise run test down. A run of length r of a sequence x=(x1,...,xn)
is a maximal strictly monotonically increasing (decreasing) subsequence (xi,...,xi+r-1},
i.e.,
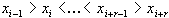
with x0 positive infinite and xn+1 negative infinite.
The expectation for the distribution of runs is derived from a simple permutation
argument and will not be reproduced here. For large n one can show that the probability to
get a run of length r is given by r/(r+1)!, hence
1/2, 1/3, 1/8, 1/30, 1/144, ...
The way the test is derived shows that this tests for correlation in the generated
sequence. The expected probabilities for the sequences reflect the independence from
correlation.
Exercises
- Generate a sequence of random numbers with parameters you think are appropriate (not the
ones listed above!). Visualize this sequence. Check whether the distribution is uniform.
- Generate a sequence of random numbers with parameters you think are appropriate (not the
ones listed above!). Store this sequence and compute the moments of the distribution.
Check whether the distribution is uniform. Compare your findings with a graphical output
(see for example the section on correlation).
- For the shift-bit-register generator generate n sequences of length m. What will be the
distribution of the expectation values?
- Use the run test to test different random number generators. Compare your findings with
a visual analysis and an analysis of the moments.
- Can you construct a modulo generator which gives an expectation value of 1/2, but all
other moments do not correspond to the uniform distribution.
Literature
- Knuth, The Art of Computer Programming, Vol. 2, Wiley, New York, 1979
- James, Comput. Phys. 60, 329-344 (1990)
- Tausworth, Math Comput, 19 201 (1965)
- T.G Lewis and W.H. Payne JACM, 20, 456-468 (1973)
- Kirkpatrick and E.P. Stoll, J. Comput. Phys. 40, 517-526 (1981)
- Park, K.W. Miller Comm. ACM 31, 1192 (1988)
- Lewis, A.S. Goodman und J.M. Miller IBM Sys. J. 8, 136 (1969)
- Anderson, SIAM Review 32, 221 (1990)
- L'Ecuyer, Comm. ACM 33, 86 (1990)
- Marsaglia, B. Narasimhan und A. Zaman, Comp. Phys. Commun. 60, 345 (1990)
- Lehmer, Proc. 2nd Symposim on Large-Scale Digital Computing Maschinery, 142, Harvard
University Press, Cambridge, 1951}
- Tausworth, Math Comput.\/, 19, 201 (1965)}
|
![]()