Percolation
Percolation seems rather simple.  Conider a simple two-dimensional lattice. Each of the lattice sites we occupy with a probability p and leave the site empty with a probability (1-p). For low p we do not expect very large clusters. A Cluster are sites that are nearest neighbours.

At large p we expect a cluster that encompasses almost all sites. Let us denote the number of sites, that participate in the largest cluster divided by the volume by P¥. For small p we should find P¥ = 0 and for large p P¥ = 1. There exists a 0 < p = pc <>< 1, such that P¥<> 0 for the frist time. At this critical point we have a (geometrical) phase transition:

pinfty.jpg (2253 Byte)

Here ß is a critical exponent.

Let nl be the number of clusters of size l, i.e. with l sites, then we can define the susceptibiltiy as

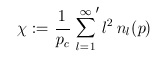
susceptibility.jpg (2884 Byte)

which deiverges as we approach the criticial probability

suscritical.jpg (2022 Byte)

We have introduced yet another exponent.
One of the most important result of percolation theory is related to universality. All presently available evidence strongly suggests, that the critical exponents depend on the dimensionality of the lattice only - but not on the lattice structure, boundary conditions and so on. The exponents for bond or site percolation, for square, triangular or honeycomb lattices etc. are the same.
next page