The group pursues research at the forefront of physics and quantitative biology with emphasis on mathematical modelling and analysis of biological data, development of computational methods, systems biology, biophysics, biomathematics, artificial intelligence and general data science methods in these fields. We develop and apply predictive models for biological and biophysical systems and their interactions at multiple scales, and create statistical methods for the analysis of the complex correlated data. We are actively engaged in joint projects with experimental biologists and physicists producing such big data resources.

Much of our current research is directed for example at combining genomic sequence, expression level information and regulation network information with structural information such as high resolution microscopy and chromosomes conformation capture data to develop models to predict biological function. Our efforts have focused on the development and application of biophysical and bioinformatics methods aimed at understanding the structural and energetic origins of chromosome interactions to reveal the underlying physical folding principles. Our work includes fundamental theoretical research and applications to problems of biological importance as well as the development of appropriate software to handle the vast amount of data.

Areas of current activity include:

Research Partners

The group has access to state-of-the-art computing facilities which we use to perform our research and offers a broad scope of educational opportunities for graduate students working in the group.

 

Modelling of the 30nm Fiber (Chromatin)

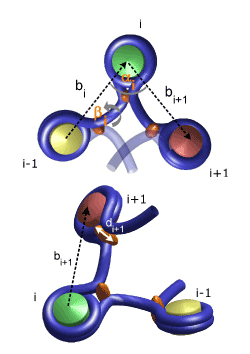
Chromatin Model
We have developed a model improving the two-angle model for interphase chromatin (E2A model). This model takes into account the cylindrical shape of the histone octamers, the H1 histones in front of the nucleosomes and the distance d between the in and outgoing DNA strands which is orthogonal to the axis of the corresponding nucleosome cylinder. Factoring these chromatin features in, one gets essential changes in the chromatin phase diagram: Not only the shape of the excluded-volume borderline changes but also the vertical distance d has a dramatic influence on the forbidden area. Furthermore, we examined the influence of H1 defects on the properties of the chromatin fiber. Thus we present two possible strategies for chromatin compaction: The use of very dense states in the phase diagram in the gaps in the excluded volume borderline or missing H1 histones which can lead to very compact fibers. The chromatin fiber might use both of these mechanisms to compact itself at least locally. Line densities computed within the model coincident with the experimental values.

Modelling of the Chromosome in Interphase

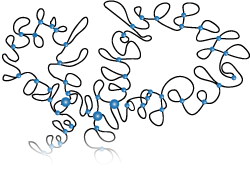
Chromatin Model
Remarkably little is known about the higher-order folding motifs of the chromatin fibre inside the cell nucleus. Folding depends among others on local gene density and transcriptional activity and plays an important role in gene regulation. Strikingly, at fibre lengths above 5 to 10 Mb the measured mean square distance <R^2> between any two points on the chromatin fibre is independent of polymer length. We propose a polymer model that can explain this levelling-off by means of random looping. We derive an analytical expression for the mean square displacement between two arbitrary beads. Here the average is taken over the thermal ensemble with a fixed but random loop configuration, while quenched averaging over the ensemble of different loop configurations - which turns out to be equivalent to averaging over an ensemble of random matrices - is performed numerically. A detailed investigation of this model shows that loops on all scales are necessary to fit experimental data.

Modelling of gene silencing (in collaboration with the group at Montpellier)

Gene silencing refers to shutting down the activity (possibly temporal) of specific genes. Temporal gene expression data is of particular interest to biologists and physicists as it represents gene expression level within a biological system over time thus modelling the living system more accurately and closely as a dynamic living system. Classical modelling on the molecular scale as well as machine learning approaches are now increasingly being used for reverse engineering gene networks from gene expression data. We develop classical models as well as hidden markov models to understand gene silencing.

Development of patterns of coarse-graining and dynamical simulations methods with application to the mechanics of the genome structure in early G1 and co-polymers

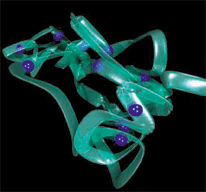
The objectives of our work are two-fold. Firstly, we want to develop systematic patterns for the coarse-graining of polymers together with the corresponding numerical algorithms applicable to a wide range of problems in biology and physics. We would like to cover technical polymers with a small degree of coarsening and bio-polymers, where a large degree of coarsening needs to be applied. The problem here is to identify the relevant length and time scales. This can best be done by applying, experimenting and validating the ideas of concrete challenging scientific questions. Here, we focus on aspects of mitosis and on co-polymers.

Mitosis is the process that facilitates the equal partitioning of replicated chromosomes into two identical groups. Before partitioning can occur, the chromosomes must become aligned so that the separation process can occur in an orderly fashion. The alignment of replicated chromosomes and their separation into two groups is a process that can be observed in virtually all eukaryotic cells. Specifically, we focus on the chromatin dynamics in the interphase which encompasses stages G1, S, and G2 of the cell cycle. We develop coarse-grained models under the perspective of a systematic coarse-graining pattern. From our previous work it has become apparent that much can be learned from studies of technical polymers. Hence, we want to investigate how we can identify and integrate out irrelevant degrees of freedom by studying co-polymers (both technical and biological).

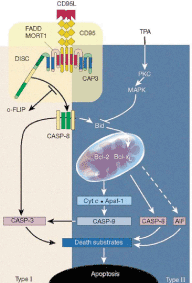
Signal Transduction Networks in Cells (in collaboration with the group of Prof. Eils)

Mathematical modelling is required for understanding the complex signaling behaviour of large signal transduction networks. Previous attempts to model signal transduction pathways have been either limited to small systems or have been based on qualitative data only. We address the complexity of a large signal transduction network by combining subsystems of different information qualities, i.e. mechanistically well-understood network parts and 'black boxes' defined by the observed input-output behaviour. The sensitivity analysis of the mathematical model was key for the identification of critical system parameters and two essential system properties: modularity and robustness. We used programmed cell death, in particular CD95-induced apoptosis, as a prototype application. The resulting data-based model provides new insight into CD95-mediated apoptosis and allows predictions as for the threshold of life and death.

 

Agent-based modelling simulations in biology

Nonlinear models in physics and biology can exhibit a number of features not known from linear ones: a particular example is chaos and the occurrence of higher level features which were not explicitly modeled. Alas, these models can in general not be solved analytically and one needs to attack them by computer simulation. In some sense we want to create artificial live by modelling our systems via agents. These agents act as independent entities that carry needs and behaviour among other characteristics as well as a model of the world (environment). Due to their interaction patterns emerge that reflect certain aspects of the real world. We study these to look for critical phenomena in these and to understand the parameter dependence of these.