Venue
This seminar in the master's degree program starts April 18th. The venue is Philosophenweg 12 / SR (3rd floor).Prerequisites
Working knowledge in Statistical PhysicsIntroduction
Early work using microscopy with fluorescent markers established that
chromosomes are not randomly organized in the nucleus. Exactly how the
chromosomes are organized could not be further revealed by this method,
even though multi-color experiments pushed the experimental boundary.
 At this stage, several models have been proposed how the genome is
physically organized in space. With the chromosome conformation capture
technology (3C) new data on the organization became available. Whereas
the information coming from the microscopy experiments gives a physical
relationship between points in space, i.e., euclidean distances on
single cell data, the 3C (and later the HiC data) yields topological
information losing the embedding into euclidean space, i.e., only
neighborhood relationships are revealed attached with a certain
probability. Furthermore, the information represents an average over
many cells. In a way, this is very much information one would classify
as of mean-field type. Thus, the challenge is to develop a model that is
consistent with the mean-field result in the sense that it succeeds to
re-embed the topological information into euclidean space.
At this stage, several models have been proposed how the genome is
physically organized in space. With the chromosome conformation capture
technology (3C) new data on the organization became available. Whereas
the information coming from the microscopy experiments gives a physical
relationship between points in space, i.e., euclidean distances on
single cell data, the 3C (and later the HiC data) yields topological
information losing the embedding into euclidean space, i.e., only
neighborhood relationships are revealed attached with a certain
probability. Furthermore, the information represents an average over
many cells. In a way, this is very much information one would classify
as of mean-field type. Thus, the challenge is to develop a model that is
consistent with the mean-field result in the sense that it succeeds to
re-embed the topological information into euclidean space.
Here you can find the slides of a talk on the subject.
Topics
- Experiments to unravel the physical structure of the genome
FiSH, 3C, Hi-C, electron microscopy, cryo-EM, ...
The key experimental techniques that have been developed to unravel the physical organization of the geonme are:
- fluorescent in situ hybridization fish protocol (FiSH) yielding euclidean distance information
- Chromosomes Conformation Capture (3C) and HiC genome wide 3C (biochemistry) yiedling topological information
- cryo-EM spatial information
Definition of the end-to-end distance measurement in FiSH experiments. The seminar talk should discuss the available data on which models rely. Specifically the following should be discussed:
- FiSH: methodology and the results for the average mean square distance as a function of the genomic (contour) distance
- 3C: methodology and the heat (contact) map for the frequency of the contacts
- HiC: methodology and the heat (contact) map. Probability distribution resulting from the heat (contact) map and the power law decay.
Literature
-
Spatially confined folding of chromatin in the interphase nucleus
Julio Mateos-Langerak, Manfred Bohn, Wim de Leeuw, Osdilly Giromus, Erik M. M. Manders, Pernette J. Verschure, Mireille H. G. Indemans, Hinco J. Gierman, Dieter W. Heermann, Roel van Driel and Sandra Goetze
PNAS March 10, 2009 vol. 106 no. 10 3812-3817 -
Comprehensive Mapping of Long-Range Interactions Reveals Folding Principles of the Human Genome
Erez Lieberman-Aiden, et al.
Science 326, 289 (2009);
DOI: 10.1126/science.1181369 -
Probabilistic modeling of Hi-C contact maps eliminates systematic biases to characterize global chromosomal architecture
Eitan Yaffe and Amos Tanay
Nature Genetics
- Models for the 30nm fibre
-
Chromatin organization - The 30 nm fiber
Sergei A. Grigoryev and Christopher L. Woodcock
Experimental Cell Research, Volume 318, Issue 12, 15 July 2012, Pages 1448-1455 -
Computational Modelling of the Chromatin Fiber
J. Langowski and Dieter W. Heermann,
Seminars in Cell and Developmental Biology, 2007 - Histone Depletion facilitates Chromatin Loops on the kbp Scale
Philipp M. Diesinger, Susanne Kunkel, Jörg Langowski and Dieter W. Heermann
Biophysical Journal, Volume 99 November 2010 2995-3001 10.1016/j.bpj.2010.08.039 - Polymer models for the 200nm fiber and beyond: Part 1
- Random Walk model (RW)
- Self-Avoiding-Walk (SAW)
- Globular State Model (GS)
- Fractal Global Model (FGS)
- Scaling laws for the above models with respect to the end-to-end-distance or the radius of gyration
-
Conformational properties of compact polymers
M. Bohn and D.W. Heermann
J. Chem. Phys. 130, 174901 (2009); DOI:10.1063/1.3126651 -
Chromatin folding: from biology to polymer models and back
Mariliis Tark-Dame, Roel van Driel, Dieter W. Heermann
doi:10.1242/jcs.077628, March 15, 2011 J Cell Sci 124, 839-845 - Polymer models for the 200nm fiber and beyond: Part 2
loopy models
HiC as well as FiSH experiments have clearly underpinned the importance of loops. Hence a polymer model that is capable of explaining these experiments needs to incorporate these.
The seminar talk should focus on the role of loops and how to incorporate them in polymer models.
A sketch of a polymer model that has build-in loops. 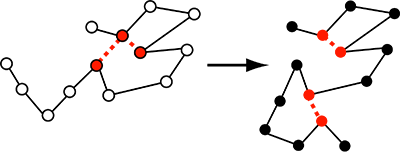
A polymer model where the loops are not static but form dynamically. - Models for chromosome territories
Chromosomes are not mixed. They are distentangled and organized in domains. This experimental observation is rather surprising. If chromosomes were just regular linear polymers, they should mix. This is because, even though they are heteropolymers, the composition from one to the other polymer is rather similar. Thus a simple entropy argument suggests a mixing of the chromosomes.
The seminar talk should discuss:
- Experimental observation
- Entropy of mixing
- Entropy of loops
- Polymer models that can explain the experimental observation
A model that shows chromosome territories as observed in experiments. Literature
-
Chromosome Territories
Thomas Cremer and Marion Cremer
2010 Cold Spring Harbor Laboratory Press -
Spatially confined folding of chromatin in the interphase nucleus
Julio Mateos-Langerak, Manfred Bohn, Wim de Leeuw, Osdilly Giromus, Erik M. M. Manders, Pernette J. Verschure, Mireille H. G. Indemans, Hinco J. Gierman, Dieter W. Heermann, Roel van Driel and Sandra Goetze
PNAS March 10, 2009 vol. 106 no. 10 3812-3817 -
Repulsive Forces Between Looping Chromosomes Induce Entropy-Driven Segregation
Manfred Bohn and Dieter W. Heermann
PLoS ONE 6(1): e14428. doi:10.1371/journal.pone.0014428 (2011)
- Models for the metaphase chromosome
Literature
- The mechanical code of chromosomes
Evidence is mounting that beside the bio-chemical aspects, the mechanics plays in important role in conformations of chromosomes. Due to nucleosomal positioning and the attachment/detachment of proteins the bending rigidity of chromosomes is influenced. This in turn regulates the kind of contacts that the chromosomes (polymers) can have with themselves and other chromosomes.
Literature
- Mechanics of chromosomes
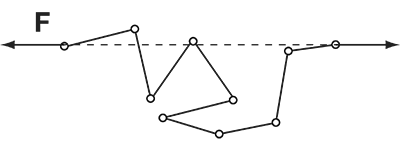
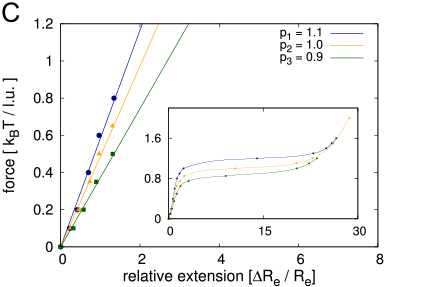
This seminar talk will discuss
- fundamental force-extension experiments
- polymer models to explain the force-extension results
The 30nm fibre (if it exists) provides the second spatial compatification of the genome. There are competing models on exactly how the 30nm fibre is formed. There is also conflicting evidence on the existence of the fibre in real nuclei. The talk discusses the models for the fibre construction. Essentially it is a stacking problem. If one considers the nucleosomes to be disks, then the question is, depending on the length and positioning of the linker between the disks, how do they stack?. The two simplest approaches are the solenoidal model and the zig-zag model.
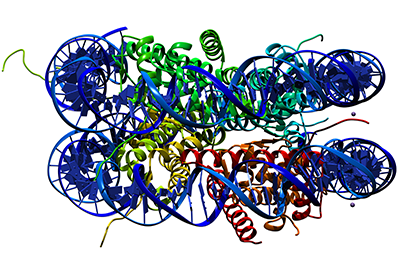
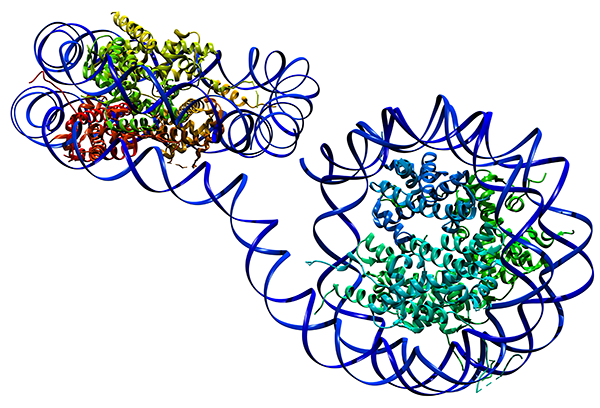
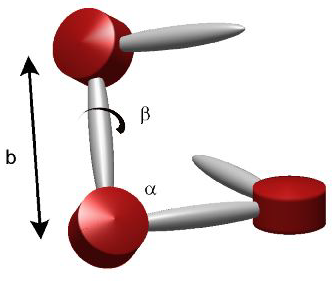
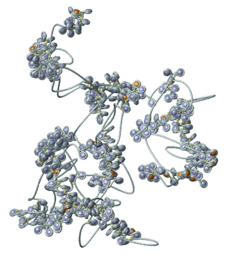
Literature
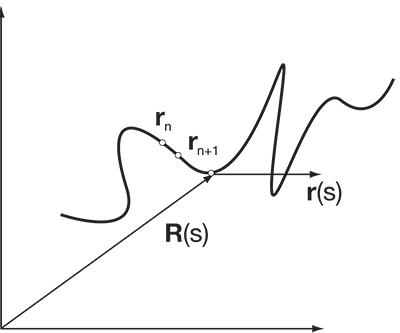
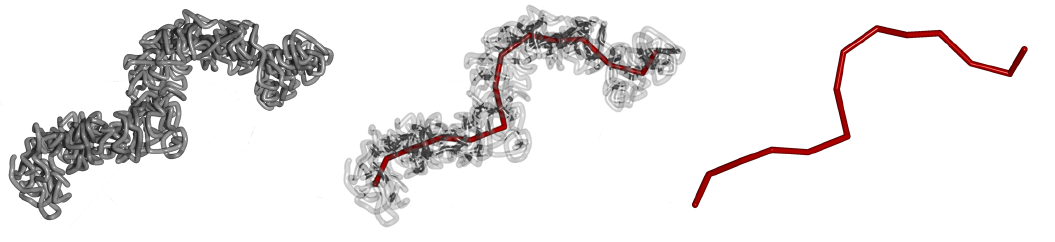
Polymers, i.e., a repeat of N monomers to form a chain, are basic for the modelling of chromosomes. The easiest such model is the random walk model (RW). This model does not take into account the excluded volume nor does it take into account other kind of repulsive or attractive forces. The self-avoiding walk model (SAW) takes the excluded volume interaction into account. The globular state model on top takes attractive interaction into account.
The seminar talk should include the statistical mechanics of polymers:
Literature
Literature
Each topic has enough substance so that it can be assigned to more than one student.
Literature (General)
-
Fractal Geometry in Biological Systems: An Analytical Approach
Philip M. Iannaccone and Mustafa Khokha
CRC Press, 1996 - Physical Nuclear Organization: Loops and Entropy, Dieter W. Heermann, Current Opinion in Cell Biology, DOI: 10.1016/j.ceb.2011.03.010 2011
- Mitotic Chromosome Structure, Dieter W. Heermann, Experimental Cell Research 318 (2012), pp. 1381-1385
More references will be supplied once the seminars have been assigned.
